Quantitative Analysis For Management Decisions Assignment Question And Answer
Are you seeking out Quantitative Analysis for Management Decisions Assignment Question and Answer? We Provide well-written and Plagiarism free content at the most affordable price. Assignmenthelpaus.com functions round the clock to accommodate academic challenges; you can also get business management Assignment help from experts before the deadline. Place your order now!
Multiple choices (one point each)
1. What is the essential condition for using the graphical method in linear programming?
a. negative variables
b. integer variables
c. only two decision variables
d. more than three variables
2. Network models such as PERT and CPM are used
a. to plan large and complex
b. to schedule large and complex
c. to monitor large and complex
d. to control large and complex
e. for all of the
3. The primary difference between PERT and CPM is that
a. PERT uses one time
b. CPM has three time
c. PERT has three time
d. with CPM, it is assumed that all activities can be performed at the same
4. If the total demand equals the total supply in a transportation problem, the problem is
a. Degenerate
b. unbalanced
c. balanced
d. infeasible
5. In a transportation problem, what indicates that the minimum cost solution has been found?
a. all improvement indices are negative or
b. all improvement indices are positive or
c. all improvement indices are equal to
d. all cells in the dummy row are
6. An assignment problem may be viewed as a transportation problem with
a. cost of $1 for all shipping
b. all supplies and demands equal to
c. only demand constraints.
d.only supply
7. If the number of filled cells in a transportation table does not equal the number of rows plus the number of columns minus 1, then the problem is said to be
a. degenerate
b. unbalanced
c. optimal
d. maximization
8. An unfeasible solution to an LP problem solved by a graphical method
a. satisfies all of the problem’s constraints
b. satisfies all of the
c. is a corner point of the feasible
d. is outside the shaded
9. If a solution to a transportation problem is degenerate, then
a. a dummy row or column must be added.
b. it will be impossible to evaluate all empty cells without removing the degeneracy.
c. there will be more than one optimal solution.
d. the problem has no feasible
10. If the total demand is greater than the total capacity in a transportation problem, then
a. the optimal solution will be
b. a dummy source must be
c. a dummy destination must be added.
d. both a dummy source and a dummy destination must be
11. The Hungarian method is
a. used to solve assignment
b. a way to develop an initial solution to a transportation
c. also called Vogel’s approximation method.
d. only used for problems in which the objective is to
12. When using the Hungarian method, an optimal assignment can always be made when every row and every column has at least one zero.
a. False
b. True
13. The first step of the maximal-flow technique is to
a. select any
b. pick any path from the start to the finish with some
c. pick the path with the maximum flow.
d. pick the path with the minimal flow.
e. pick a path where the flow going into each node is greater than the flow coming out of each node.
14. In which technique do you connect the nearest node to the existing solution that is not currently connected?
a. maximal tree
b. shortest route
c. maximal flow
d. minimal flow
15. In the shortest-route technique, the objective is to determine the route from an origin to a destination that passes through the fewest number of other
a. True
b. False
16. If a linear program is unbounded, the problem probably has not been formulated Which of the following would most likely cause this?
a. A constraint was inadvertently
b. An unnecessary constraint was added to the
c. The objective function coefficients are too
d. The objective function coefficients are too
17. Adjusting the flow capacity numbers on a path is an important step in which technique?
a. minimal flow
b. maximal flow
c. shortest route
18. When PERT is used and probabilities are found, one of the assumptions that is made is that
a. all activities are on the critical
b. activity times are
c. all activities have the same
d. the project variance is equal to the sum of the variances of all activities in the
e. all of the
19. If a project is to be crashed at the minimum possible additional cost, then the first activity to be crashed must be
a. on the critical
b. the one with the shortest activity
c. the one with the longest activity
d. the one with the lowest
20. If all of the decision variables require integer solutions, the problem is
a. a pure integer programming type of
b. a dummy type of
c. a mixed-integer programming type of problem
21. Which of the following factors apply in a goal programming problem?
a. All variables are required to have integer
b. Some of the variables are required to have integer
c. More than one objective is
d. The objective is to maximize the total of the deviational variables
Workout (3 points each)
1. Discuss the properties and assumptions of linear programming problems
2. Maximize
5X1 + 7X2
s.t.X1 < £ 6
2X2 + 3X2 £ 19
X2 + X2 < 8
X2 , X2 > 0
Solve using
a. simplex method
b. verify your answer using graphical method
c. verify your answer using solver table on excel
3. A firm makes two types of furniture chairs and tables. The contribution for each product to objective function is birr 20 per chair and birr 30 per table Both products are processed on three Machines M1, M2 and M3. The time required (in hours) by each product and total time available per week on each machine are as follows:
| Machine | Chair | Table | Available time |
| M1 | 3 | 3 | 36 |
| M2 | 5 | 2 | 50 |
| M3 | 2 | 6 | 60 |
How should the manufacturer schedule his production in order to maximize contribution?
4. Consider the following transportation problem:
| Store 1 | Store 2 | Store 3 | Store 4 | Supply | |
| Plant 1 | 19 | 30 | 50 | 10 | 7 |
| Plant 2 | 70 | 30 | 40 | 60 | 9 |
| Plant 3 | 40 | 8 | 70 | 20 | 18 |
| Demand | 5 | 8 | 7 | 14 | 34 |
a. Use North-West Corner (NWC) Method, Least Cost Method (LCM), and Vogel’s Approximation (or penalty) Method (VAM), to obtain the initial basic feasible solution and show the corresponding total transportation cost.
b. Reformulate this problem as a general linear programming
c. Use stepping stone and modified distribution (MODI) to calculate the optimum transportation cost
5. A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. According to this table, Job 1 will cost $15 if done by Employee A, $20 if it is done by Employee B, and so The manager has stated that his goal is to develop a set of job assignments that will minimize the total cost of getting all four jobs done. It is further required that the jobs be performed simultaneously, thus requiring one job being assigned to each employee. Although the manager recognizes that this problem can be solved using the simplex routine, he also knows that he can solve the problem by hand using the assignment method.
Job Costs for Each Possible Pairing
| Employees | |||||
| Abdella | Bontu | Chanie | Debela | ||
| 1 | $15 | 20 | 18 | 24 | |
| 2 | 12 | 17 | 16 | 15 | |
| Job | 3 | 14 | 15 | 19 | 17 |
| 4 | 11 | 14 | 12 | 13 | |
Required:
Formulate a linear Programming problem
- Which salesperson should be assigned to each region to minimize total time?
- Identify the optimal assignments and compute total minimum time. Use the Hungarian Method
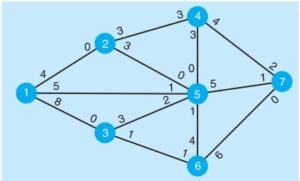
6. Petroleum refining company is designing a new plant to produce diesel fuel.
Figure below shows the network of the main processing centers
along with the existing rate of flow (in thousands of gallons of fuel). The management at the company would like to determine the maximum amount of fuel that can flow through the plant, from node 1 to node 7
Using the maximal flow technique, determine the amount of fuel shipped through the network.
7. To complete the wing assembly for a new helicopter, Ethiopia has laid out the major steps and seven activities These activities have been labeled A through G in the following table, which also shows their estimated completion times (in weeks) and immediate predecessors. Determine the expected time and variance for each activity. Determine the critical path for the entire activities and the expected completion time.
8. Consider the 0–1 integer programming problem that follows:
Maximize
50X1 + 45X2 + 48X3
subject to19X1 + 27X2 + 34X3 <80
22X1 + 13X2 + 12X3 <40
X1, X2, X3 must be either 0 or 1
Solve the problem using Excel solver