Review Assignment Questions and Answers
Are you looking out for your Review Assignment Questions and Answers? Grab the opportunity to find fresh assignment answers related to all subjects in your Academic. Assignmenthelpaus.com is No.1 Assessment Answers provider in Australia. The 3000+ MBA/PhD level academic writers offer case study writing services, dissertation writing, custom essays and homework. You can clear all your assignments or our service related queries through our 24×7 online chat support facility anytime. We can provide you with a free Turnitin report regarding our help material.
Chapter Two: LP Model formulation and solution (Graphic method)
1. ABC Company supplies fruit juice and juice blends to wholesale grocers. A list of the firm’s products and revenue per ounce is shown in the following table:
| Product | Revenue per ounce |
| Apple juice | 0.09$ |
| Grape juice | 0.06$ |
| Cranberry juice | 0.05$ |
| Apple-grape juice | 0.07$ |
| Apple-cranberry juice | 0.08$ |
| All-in-one juice | 0.10$ |
The apple-grape juice is 70% apple juice and 30% grape juice. The apple-cranberry juice is 60%apple juice and 40% cranberry juice, and the all-in-one juice is 50% apple, 20%grape, and the rest cranberry juice. The company has 200 gallons of apple juice, 100 gallons of grape juice and 150 gallons of cranberry juice on hand, and the owner wants to know how many containers of each product to prepare in order to maximize profit. Cost per ounce for apple juice is 0.02$, for grape juice 0.04$, and for Cranberry juice 0.03$. All products are sold in 64 oz. containers. The apple-cranberry juice is also sold in a one-quart size. The company has an order for 10 containers of apple juice and 12 containers of the apple-cranberry one-quart size that must be filled from current supplies. Formulate linear programming model of this problem.
2. Back Savers is a company that produces backpacks primarily for students. They are considering offering some combination of two different models—the Collegiate and the Mini. Both are made out of the same rip-resistant nylon fabric. Back Savers has a long-term contract with a supplier of the nylon and receives a 5,000-squarefoot shipment of the material each week. Each Collegiate requires 3 square feet while each Mini requires 2 square feet. The sales forecasts indicate that at most 1,000 Collegiates and 1,200 Minis can be sold per week. Each Collegiate requires 45 minutes of labor to produce and generates a unit profit of $32. Each Mini requires 40 minutes of labor and generates a unit profit of $24. Back Savers has 35 laborers that each provides 40 hours of labor per week. Management wishes to know what quantity of each type of backpack to produce per week.
a. Formulate and solve a linear programming model for this problem.
b. Use the graphical method to solve this model.
c. Solve for Slack
3. Blue Ridge Hot Tubs manufactures and sells two models of hot tubs: the Aqua-Spa and the Hydro-Lux. Howie Jones, the owner and manager of the company, needs to decide how many of each type of hot tub to produce during his next production cycle. Howie buys prefabricated fiberglass hot tub shells from a local supplier and adds the pump and tubing to the shells to create his hot tubs. (This supplier has the capacity to deliver as many hot tub shells as Howie needs.) Howie installs the same type of pump into both hot tubs. He will have only 200 pumps available during his next production cycle. From a manufacturing standpoint, the main difference between the two models of hot tubs is the amount of tubing and labor required. Each Aqua-Spa requires 9 hours of labor and 12 feet of tubing. Each Hydro-Lux requires 6 hours of labor and 16 feet of tubing. Howie expects to have 1,566 productions labor hours and 2,880 feet of tubing available during the next production cycle. Howie earns a profit of $350 on each Aqua-Spa he sells and $300 on each Hydro-Lux he sells. He is confident that he can sell all the hot tubs he produces. The question is, how many Aqua-Spas and Hydro-Luxes should Howie produce if he wants to maximize his profits during the next production cycle?
4. The following table summarizes the key facts about two products, A and B, and the resources, Q, R, and S, required to produce them.
| Resource | Resource Usage per Unit Produced | ||
| Product A | Product B | Resource Available | |
| Q | 2 | 1 | 2 |
| R | 1 | 2 | 2 |
| S | 3 | 3 | 4 |
| Profit/unit | 3000$ | 2000$ | |
Holding all the assumptions of linear programming, formulate and solve a linear programming model for this problem.
5. The Apex Television Company has to decide on the number of 27″ and 20″ sets to be produced at one of its factories. Market research indicates that at most 40 of the 27″ sets and 10 of the 20″ sets can be sold per month. The maximum number of work-hours available is 500 per month. A 27″ set requires 20 work-hours and a 20″ set requires 10 work-hours. Each 27″ set sold produces a profit of $120 and each 20″ set produces a profit of $80. A wholesaler has agreed to purchase all the television sets produced if the numbers do not exceed the maxima indicated by the market research.
a. Formulate and solve a linear programming model for this problem.
b. Solve for slack
6. An individual investor has Birr 70,000 to divide among several investments. The alternative investments are municipal bonds with an 8.5% return, certificates of deposits with a 10% return, Treasury bill with a 6.5% return, and income bonds with a 13% return. The amount of time until maturity is the same for each alternative. However, each investment alternative has a different perceived risk to the investor; thus it is advisable to diversify. The investor wants to know how much to invest in each alternative in order to maximize the return. The following guidelines have been established for diversifying the investment and lessening the risk perceived by the investor.
- No more than 20% of the total investment should be in an income bonds.
- The amount invested in certificates of deposit should not exceed the amount invested in other three alternatives.
- At least 30% of the investment should be in treasury bills and certificates of deposits.
- The ratio of the amount invested in municipal bonds to the amount invested in treasury bills should not exceed one to three.
- The investor wants to invest the entire Birr 70,000
Required:
- Formulate a LP model for the problem.
- Solve using the simplex method.
7. A manager of a firm that assembles various electronic items wants to establish an optimal production plan for making Tape decks. The manager has obtained the pertinent information which is shown in the table below:
| Item | Assembly time | Inspection time | Packaging time | cost per unit | Price per unit |
| Type A | 3 | 5 | 2 | 65 | 90 |
| Type B | 4 | 4 | 4 | 70 | 110 |
| Type C | 2 | 4 | 5 | 50 | 85 |
| Available time | 60 hours | 72 hours | 96 hours |
Required
a. Formulate the above LPP if the manager wants to maximize the total contribution of the output to profit.
b. Write the problem in standard form and develop the initial tableau.
c. Determine the optimal solution using simplex. Identify the variables that are in solution at the optimum and their values.
d. Identify the shadow prices and interpret each shadow price.
Chapter Three: Integer Programing
8. A tailor makes wool tweed sport coats and wool slacks. He is able to get a shipment of 150 square yards of wool cloth from Scotland each month to make coats and slacks, and he has 200 hours of his own labor to make them each month. A coat requires 3 square yards of wool and 10 hours to make, and a pair of slacks requires 5 square yards of wool and 4 hours to make. The tailor earns $50 in profit from each coat he makes and $40 from each pair of slacks. He wants to know how many coats and pairs of slacks to produce to maximize profit.
a. Formulate an integer linear programming model for this problem.
b. Determine the integer solution to this problem by using branch & bound Method. Compare this solution with the solution without integer restrictions and indicate whether the rounded-down solution would have been optimal.
Chapter Four: Transportation
9. A company imports goods at two ports: Lisbon and Le Havre. Shipments of one of its products are made to customers in Paris, Berlin, London and Milan. For the next planning period, the supplies at each port, customer demands and the shipping costs ($) per case from each port to each customer are as follows:
| Port | Customer | Port Supply | |||
| Paris | Berlin | London | Milan | ||
| Lisbon | 2 | 6 | 6 | 2 | 5 000 |
| Le Havre | 1 | 2 | 5 | 7 | 3 000 |
| Demand | 1 400 | 3 200 | 2 000 | 1 400 | |
a. Develop a network model of the distribution system for this problem.
b. Test the necessary assumptions for to use transportation model.
c. Develop
d. Solve the problem to determine the minimum cost-shipping schedule.
e. Suppose that the entries in the table represent profit per unit produced at plant i and sold to warehouse j. How does the model change from that in part (b)?
10. Consider the following network representation of a transportation problem:
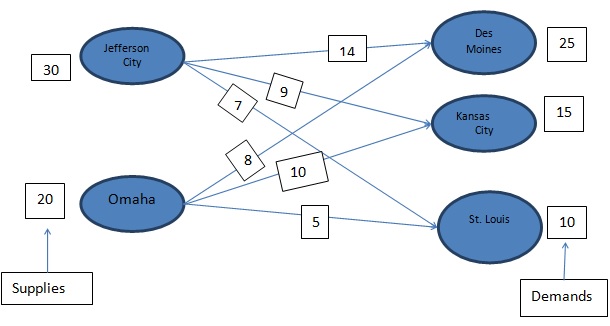
The supplies, demands and transportation costs per unit are shown on the network.
a. Test the necessary assumptions to use transportation model.
b. Develop a linear programming model for this problem; be sure to define the variables in your model.
c. Solve the linear program to determine the optimal solution.
Chapter Five: Inventory Model
11. Suppose that the R&B Beverage Company has a soft drink product that shows a constant annual demand rate of 3600 cases. A case of the soft drink costs R&B $3. Ordering costs are $20 per order and holding costs are 25% of the value of the inventory. R&B has 250 working days per year, and the lead -time is 5 days. Identify the following aspects of the inventory policy:
a. Economic order quantity
b. Reorder point
c. Cycle time
d. Total annual cost
12. Westside Auto purchases a component used in the manufacture of automobile generators directly from the supplier. Westside’s generator production operation, which is operated at a constant rate, will require 1000 components per month throughout the year (12,000 units annually). Assume that the ordering costs are $25 per order, the unit cost is $2.50 per component, and annual holding costs are 20% of the value of the inventory. Westside has 250 working days per year and a lead time of 5 days. Answer the following inventory policy questions:
a. What is the EOQ for this component?
b. What is the reorder point?
c. What is the cycle time?
d. What are the total annual holding and ordering costs associated with your recommended EOQ?
For REF… Use: #getanswers2001679

